ゲームの代数的なひろがり

- 工学部 基礎教育センター
- 助教 入江 佑樹
- ホームページ »
- 山梨大学研究者総覧へ »
美しいものを見つけることを目指して, 対称性について研究しています. 数学において対称性は「群」というもので記述されます. 群は対称性の本質を取り出したものであり, 代数構造という抽象的なものです. 抽象的な群を具体的に表現することで, 現実世界の対称性が現れます. 群はものごとの背後に隠れていることが多く, 隠れた群を見つけることで, 新たな美しさを発見することが私の研究目標です.
特に「ゲーム」の背後に隠れている群を研究しています. また群の中でも, 奇跡的に存在する「散在型単純群」と, 母なる群とでも呼べる「対称群」を中心に研究をしてきました. 以下, 具体的に研究内容を二つ紹介します.
(1) ゲームと群の表現
将棋などのゲームは, 数学では「組合せゲーム」と呼ばれます. この組合せゲームの一種に「マヤゲーム」があります (下で紹介). マヤゲームをただ眺めていても, 対称性を記述する, 群との関係は見えません. しかし近年マヤゲームと, 対称群の表現との間の密接な関係が分かってきました. さらに両者の関係を通して, 従来とは異なる視点が得られ, 群とゲームの双方に対する新たな発見につながっています.
マヤゲーム: 数字の振られたマス目とコインで遊ぶ, 二人対戦ゲーム. 二人のプレイヤーは交互にコインを小さい数の空きマスへ移動 (図では 6 のコインを 3 へ移動). 先にコインを動かせなくなった方の負け (上の例だと 0 1 2にコインが置かれた状態にした方の勝ち).
(2) ゲームとデザイン
群と深く関係する「デザイン」と呼ばれる構造があります. 2 点を通る直線は 1 本あります. 身の回りの空間には無限個の点がありますが, 同様の性質を有限個の点で実現するものがデザインであり, 次が例です.
デザインの例: 図には7点あり, どの2点を通る線も 1 本. たとえば 0 と 6 の 2 点を通る線は 0 1 6. また 1 と 4 を通る線は 1 2 4 (円で書かれた部分).
デザインは, 実はゲームの必勝法とも深く関係しています. 特に, ある散在型単純群と関係するデザインと対応するゲームの間には, 不思議な現象が起こっており, 現在はこの現象の解明を目指して研究をしています.
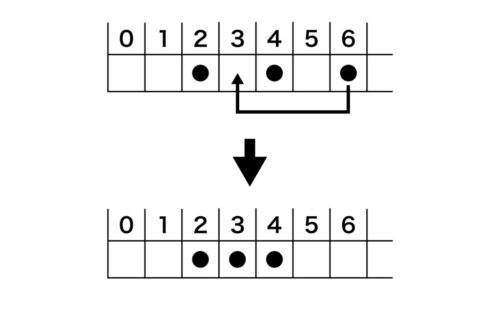
マヤゲーム
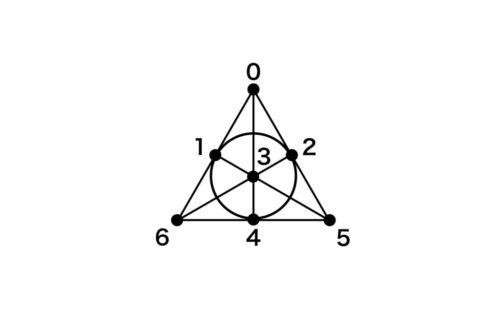
デザインの例
